Gray-Scott Model at F 0.0260, k 0.0550
These images and movie demonstrate the behavior of the Gray-Scott reaction-diffusion system with σ=Du/Dv=2 and parameters F=0.0260, k=0.0550.
Rings grow, remaining fairly symmetrical to a radius of over 1.0 lu. Patterning develops in their interior, while outer edges become ragged but remain continuous. After filling the space, the pattern organizes into mazelike connected closed loops (negative worms and the occasional solitary negative soliton).
After about 10,000 tu, parallel ridges pulse in a coordinated fashion. Occasional extinctions at junctions continue to occur, causing the pattern to continue changing. The structure tends towards longer, straighter lines and 120o angles.
By 250,000 to 500,000 tu, most of the field is "quiet" (not pulsing) for most of the time, but junction events continue to happen. Some of these set off a long-lasting oscillation with the junction as its center; others happen fairly peacefully. One junction was observed initiating such a wave 11 times in succession with a regular cycle of about 825,000 tu.
This goes on for about 5,000,000 tu but appears to settle down within the next 5 to 10 million.
Categories: Pearson γ; Wolfram 3 (glossary of terms)
 increase F increase F
 | |||
 decrease k  |


|
15 frames/sec.; each fr. is 40 iter. steps = 20 tu; 1800 fr. total (36,000 tu) | 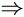 increase k 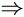
|

|


| ||
 decrease F decrease F
 |
In these images:
- Color indicates level of u, ranging from purple (lowest u values) through blue, aqua, green, yellow and pink/red (highest u values)
- Areas where u is increasing are lightened to a light pastel tone; where u is decreasing the color is vivid.
- In areas where u is changing by less than ±3×10-6 per tu, an intermediate pastel color is seen. This includes areas that are in steady state or equilibrium.
''tu'' is the dimensionless unit of time, and ''lu'' the dimensionless unit of length, implicit in the equations that define the reaction-diffusion model. The grids for these simulations use Δx=1/143 lu and Δt=1/2 tu; the system is 3.2 lu wide. The simulation meets itself at the edges (periodic boundary condition); all images tile seamlessly if used as wallpaper.
Go back to Gray-Scott pattern index
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2015 Nov 07.
 s.27
s.27